Difference between revisions of "Manual/Plugins/List/Fill Area"
Jump to navigation
Jump to search
(Created page with "Detects an area from the active selection and fills it with a dense graph. This plugins inserts a polygon in the active document. Can be useful to create knots with some rota...") |
|||
| Line 18: | Line 18: | ||
; Grid Size | ; Grid Size | ||
: The size of the grid used to fill the area. | : The size of the grid used to fill the area. | ||
| + | |||
| + | ==Explanation of the polygon algorithms== | ||
| + | |||
| + | Here are illustrated how the polygon algorithms affect the outcome of the fill. | ||
| + | |||
| + | ===Convex Hull=== | ||
| + | <gallery> | ||
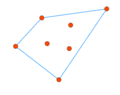
| + | File:Plugin_Fill_Area_Example1.png|Start with a set of vertices, edges between them are disregarded. | ||
| + | File:Plugin Fill Area Example2.png|The algorithm calculates the convex hull. | ||
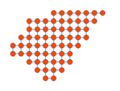
| + | File:Plugin_Fill_Area_Example3.png|The area inside the convex hull is filled. | ||
| + | </gallery> | ||
| + | |||
| + | |||
| + | ===Single Edge Loop=== | ||
| + | <gallery> | ||
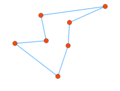
| + | File:Plugin_Fill_Area_Example4.png|Start with a predefined polygon. There must not be extra edges or missing edges. | ||
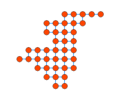
| + | File:Plugin_Fill_Area_Example5.png|The area inside the polygon hull is filled. | ||
| + | </gallery> | ||
Revision as of 18:19, 4 June 2013
Detects an area from the active selection and fills it with a dense graph.
This plugins inserts a polygon in the active document. Can be useful to create knots with some rotational symmetry.
Parameters
- Delete original selection
- If checked, the nodes selected when this plugin is triggered will be removed from the graph.
- Polygon
- Algorithm used to detect the area to be filled:
- Convex Hull
- The area will be the minimum convex polygon that contains all the nodes.
- Single Edge Loop
- The selected nodes are assumed to be all connected by a single loop of edges.
- If this precondition is not met, the result will be inaccurate.
- Grid Size
- The size of the grid used to fill the area.
Explanation of the polygon algorithms
Here are illustrated how the polygon algorithms affect the outcome of the fill.
Convex Hull